Teoria Sterowania

Obserwator Luenbergera pełnego rzędu

Laboratorium problemowe, IV rok AGH

1. Wprowadzenie

Dany jest obserwowalny system liniowy n-tego rzędu

z m-wymiarowym równaniem wyjścia

Celem ćwiczenia jest skonstruowanie systemu zwanego obserwatorem Luenbergera pełnego rzędu, który na podstawie znanej trajektorii wyjścia y i sterowania u systemu (1),(2) generuje trajektorię w z upływem czasu zmierzającej do nieznanej trajektorii stanu x systemu (1),(2).

Obserwator ten ma postać systemu liniowego n-tego rzędu

przy czym błąd obserwacji stanu zanika z czasem

przy dowolnych warunkach początkowych x(0), w(0) i dowolnym sterowaniu u.

Po przekształceniach można pokazać, że konstrukcja obserwatora polega na dobraniu macierzy G w taki sposób, żeby macierz F była asymptotycznie stabilna

2. Zadanie I

Dany jest system oscylacyjny postaci (1),(2) z macierzami

.

Konstruując obserwator na początku należy wyrazić elementy macierzy G poprzez wartości własne λ₁, λ₂ macierzy F

G jest 2-elementowym wektorem pionowym oraz .

Po podstawieniu do (3) otrzymujemy

Następnie rozwiązując lewą stronę i przekształcając prawą do postaci wielomianu charakterystycznego otrzymujemy

Porównując współczynniki przy s oraz wyrazy wolne dostajemy

Ostatecznie

W ćwiczeniu przyjęto, że wartości własne są sprzężone tzn. λ₁ = λ₂ = λ.

Modelowanie układu bez zakłóceń

Obserwator zamodelowano przy użyciu pakietu Matlab-Simulink

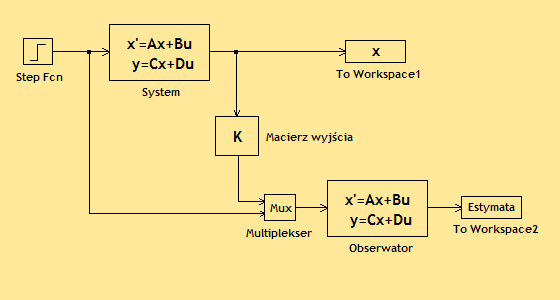
Do zamodelowania systemu i obserwatora wykorzystano standardowe bloczki pakietu Symulink. Aby mieć możliwość obserwacji błędu e=estymata-x należało wyprowadzić zmienną x (stan systemu). W tym celu system podzielono na dwa bloczki:

- pierwszy State-space zawierający równanie stanu systemu z macierzami

- drugi Matrix-gain zawierający macierz wyjścia systemu C= [0 1].

Do zamodelowania obserwatora skorzystano z bloczka State-space z macierzami

Ponieważ bloczek State-space posiada jedno wejście skorzystano z multipleksera Mux. Do przestrzeni Matlaba wysyłane były zmienne x oraz estymata. Na wejście układu podawany był skok jednostkowy za pomocą bloczka Step Fcn.

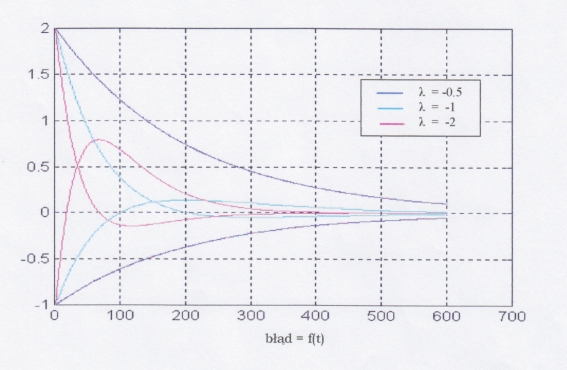
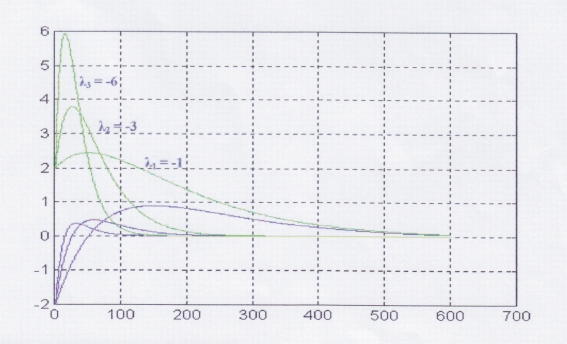
Doświadczenie przeprowadzono dla różnych wartości λ. Obserwator startował z innych warunków początkowych niż system. Wykres poniżej przedstawia błędy obserwacji.

Z wykresu widać, że obserwator jest szybszy (błąd szybciej zmierza do zera) dla bardziej ujemnych wartości własnych λ.

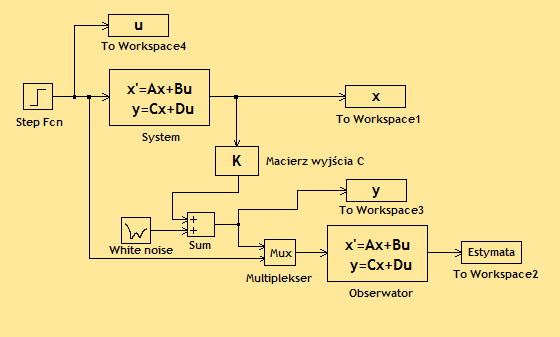
Modelowanie układu z zakłóceniami

W celu sprawdzenia odporności obserwatora na zakłócenia zmodyfikowano poprzedni układ wprowadzając szum, który dodaje się do sygnału wyjściowego.

Model systemu z obserwatorem zrealizowany przy pomocy pakietu Matlab-Simulink.

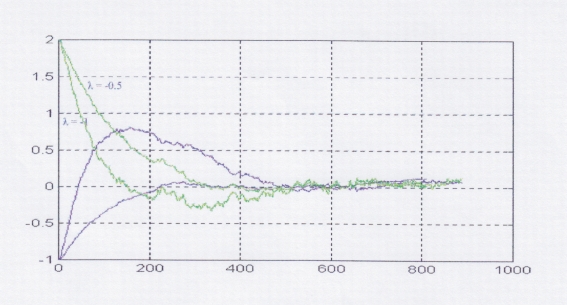
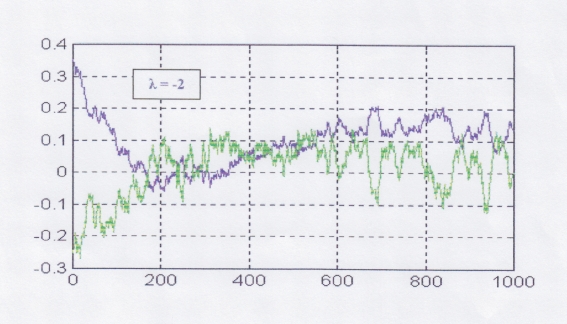
Z wykresu widać, że pomimo zakłóceń obserwator odtwarza stan i błąd dąży do zera. Jednak jeśli wartości własne macierzy F są bardziej ujemne, wtedy rośnie wrażliwość na zakłócenia. Poniżej znajduje się przypadek, gdy obserwator stracił swoje właściwości – błąd nie zmierza do zera.

3. Zadanie II

Dany jest system

Który po sprowadzeniu do równań stanu (1),(2) daje się opisać następującymi macierzami

System ten jest obserwowalny. Podobnie jak w poprzednim zadaniu konstruujemy obserwator poprzez wyrażenie elementów macierzy G za pomocą wartości własnych λ₁, λ₂ macierzy F

G jest 2-elementowym wektorem pionowym oraz .

Po podstawieniu do (3) otrzymujemy

Następnie rozwiązując lewą stronę i przekształcając prawą do postaci wielomianu charakterystycznego otrzymujemy

Porównując współczynniki przy s oraz wyrazy wolne dostajemy

W ćwiczeniu przyjęto, że wartości własne są sprzężone tzn. λ₁ = λ₂ = λ.

Modelowanie układu bez zakłóceń

System z obserwatorem zrealizowano przy użyciu modelu z zadania poprzedniego zmieniając odpowiednio macierze A,B,C,G. Wykres poniżej ilustruje wyniki, z których widać, że obserwator jest szybszy (błąd szybciej zmierza do zera) gdy wartości własne macierzy F są bardziej ujemne.

Modelowanie układu z zakłóceniami

W celu zbadania odporności obserwatora na zakłócenia, do układu wprowadzono szum tak jak dla zadania I.

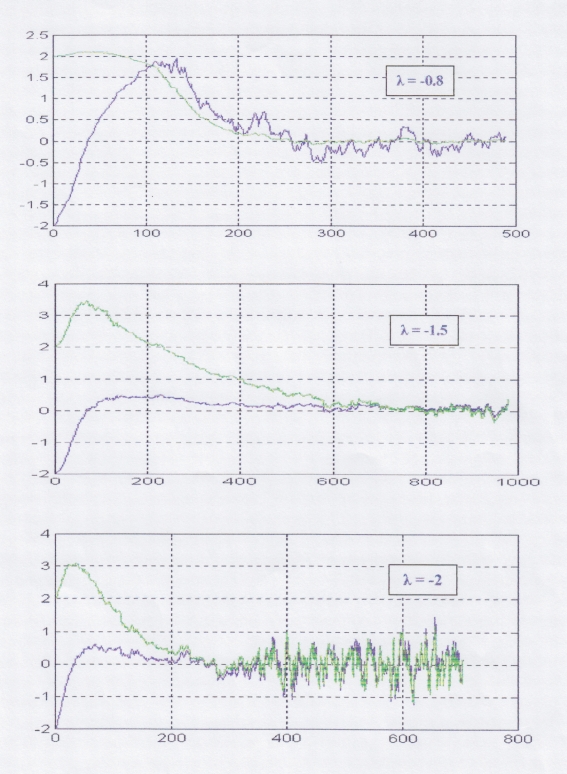
Wyniki dają te same wnioski co dla systemu oscylacyjnego z zdania I. Obserwator dobrze odtwarza stan systemu, lecz gdy wartości własne macierzy F maleją znacznie, obserwator traci swe zdolności (ostatni wykres). Zadając wartości własne macierzy F należy wybrać pewne optymalne wartości, dla których obserwator działa prawidłowo.